Audio tech in games is rarely particularly interesting. Sadly, most of it seems to have been made into commodity over the last couple of decades. Once in while, some games have very clever audio tech, and in this case it was NieR:Automata’s tone filter which caught my attention. The blog post explaining this tech is found here. If you haven’t played the game, it is highly recommended to read the post and watch the videos to understand what it’s doing. That saves me a lot of explanation. Their blog is very sparse on technical implementation details, but I wanted to try recreating it as there was just enough high-level detail in there to get me started.
Outside graphics, I’ve done a fair bit of audio programming in the past. It’s been too long since I did any significant audio DSP programming.
In short, the goal of the filter is to attempt to turn normal high-fidelity soundtracks into something with an 8-bit feel on-demand. Being able to introduce dynamic aspects to the music with a pure filter is interesting.
The tone filter as explained
The goal of the filter is to extract musical notes, and emphasize them. By having a few notes playing with a classic waveform like square or saw waves, we can recreate a retro 8-bit feel.
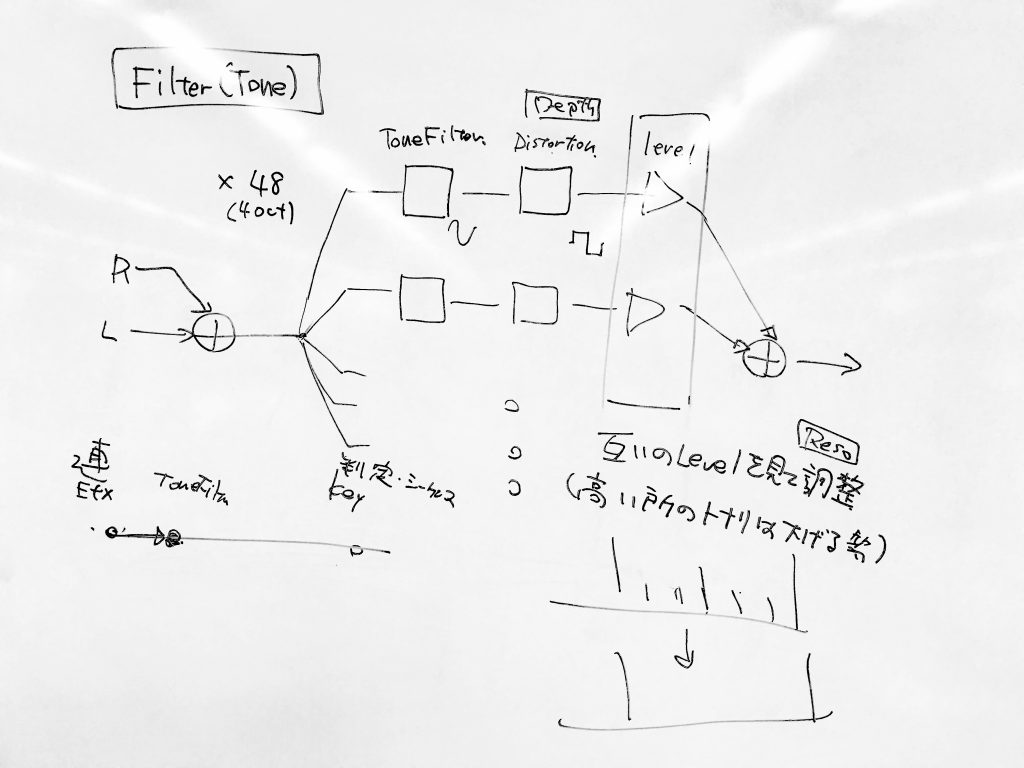
The blog describes 48 filters, spanning 4 octaves. Each octave in the (western music) scale is divided into 12 tones. What I deduced from this is that the 48 filters should be 48 very sharp bandpass filters.
A theoretically perfect bandpass filter will output a pure sine wave if the tone exists, and nothing if it doesn’t.
The distortion is tough to do well, and I spent a lot of time fiddling with this. We want to try making the sine wave become something like a square wave. I tried many variants but I ended up with something very simple like
https://www.desmos.com/calculator/qvymx5qf8t
If you’ve done HDR tone-mapping, this formula will look very familiar to you. Sometimes cross-domain knowledge comes in handy.
After distorting, there is the levelling stage, which I spent a lot of time fiddling with. Basically, if we run this system as is, we end up with a ton of noise in the signal with all the chromatic tones playing over each other. Needless to say, this sounded absolutely terrible.
There are little to no details on how this should be implemented, so I tried a very crude model which seems to work reasonably well. Basically, each of the 48 channels have a running power estimate which is computed right after the filter. We can compare that against the running power estimate of the unfiltered audio. This lets us get an idea how much of the audio energy is concentrated into each individual tone. If the energy is low enough, it falls off in a power-of-4 fashion to avoid leaking in audio from completely unrelated tones. Percussion sounds will generally have energy in almost the entire audio spectrum, and we need to filter that out as well as we can. If the ratio is too high, we just cap it. This is the fiddly part. There’s a lot of magic constants to tweak to get it sounding pleasing.
At the end we mix our mono output signal back into the original audio, and when it works well, it gives a nice harmonic edge. I believe it’s reasonably close to the original game now. Here’s an example from the NieR:Automata OST. I’m visualizing all the 48 bands, and the colors are:
- Blue: Below threshold, severely muted.
- Green: Over threshold, should be heard.
- Red: Saturated, hitting max threshold.
The tones in one octave form one row, and the four octaves are stacked on top of each other. The top-left starts at A3 – 220 Hz. If you know some music theory, maybe you can figure out which key the tune is in? 🙂
Implementation
First we mix stereo down to mono. This is kind of trivial. Just take the average of left and right channels.
Ultra-sharp bandpass, resonance filters
I went through a few failed iterations to get here. My first attempts were to do all of this in the frequency domain with FFTs, but that plan failed very quickly. What I ended up with in the end was a simple biquad resonance filter. This filter is characterized by having two zeroes and two poles in DSP parlance, or in other words, FIR (finite impulse response) and IIR (infinite impulse response). In code, this would look something like:
y[t] = n0 * x[t] + n1 * x[t - 1] + n2 * x[t - 2] - d0 * y[t - 1] - d1 * y[t - 2]In the Z-domain, this looks like
H(z) = 1/n0 * (1 + z^-1 * n1/g + z^-2 * n2/g) / (1 + z^-1 * d0 + z^-2 * d1)The zeroes and poles occur where the roots of the polynomials go to zero in the numerator and denominator respectively. Basically, I designed the filter by deliberately placing zeroes and poles in the Z-domain, factoring the expressions out and converting it back to a normal FIR and IIR form.
I placed a zero at DC and the Nyquist frequency (w = pi). The poles were placed very close to the unit circle at w = +/- 2 * pi * freq / samplerate, and amplitude 0.9999. Then I evaluated the filter response at the resonance frequency and adjusted the FIR portion of the filter so that we got an estimated unit gain at the resonance frequency.
Basically, the frequency response at the resonance frequency will be very close to dividing by zero, so near-infinite response, but not quite. Numerical stability can easily throw off the filter if we’re not careful. This is one of the major issues with IIR filters in general. I initially tried an 8-pole filter but it was impossible to get this stable even in FP64, so I just gave up and tried a simple biquad instead which worked just fine.
SIMD
Since we’re doing 48 IIR filters in parallel, this was a perfect case for SIMD optimizations. I made everything into a struct-of-arrays (SoA) form, and just vectorized the scalar IIR filter directly. Normally, small IIR filters are tricky to vectorize since there are inter-dependencies between samples, but not here.
I optimized the filter in NEON, SSE1 and AVX and got a very nice performance boost, more on that later.
This would have been a great case for ISPC, but I considered it a too large dependency for something simple like this.
Distortion
The distortion function must be nicely SIMD-friendly and not too expensive. I landed on the classic x/(1+abs(x)) operator. The divide can be done fast with reciprocal estimations. We didn’t need high accuracy.
Slight low-pass
After we have mixed together the 48 distorted streams, we run a weak low-pass filter on top to remove some of the harshest harmonics. This is done with a trivial 1-pole IIR filter.
Performance
I tested performance on a Ryzen 7 1800x @ 3.8 GHz as well as a high-end phone (Galaxy S9 Exynos) to measure NEON performance. The benchmark pushes 20 million white noise samples through the filter and then times the result. The test doesn’t take that long, so this should be assumed to be absolute peak performance without any thermal / power consideration. The results below are given in samples processed per second. Normal audio clips are 44.1 kHz, so 0.041 M/s should correspond to 1x real-time performance. The C++ version is written without any intrinsics with -O3 -ffast-math. The SIMD versions are written with the standard intrinsics.
| Chip | C++ | SSE | AVX | AArch64 NEON |
| Samsung Exynos 9810 | 1.8 M/s | 6.8 M/s | ||
| Ryzen 7 1800x @ 3.8 GHz | 3.6 M/s | 7.1 M/s | 11.5 M/s |
Basically, we’re 100x realtime performance here, even on a mobile CPU, nice. I’m surprised how close the performance ended up when comparing SSE and NEON. I didn’t see any auto-vectorization activate in the C++ variant, so I wonder what is going on with just 2x scaling in SSE. I got similar results on MSVC and GCC for what it’s worth … NEON gets close to ideal 4x scaling though, nice.
This uses quite a bit of processing power, so we can’t run wild with effects like this right now. But I look forward to being able to take advantage of systems like this for even more precise operations in the future.
The original implementation probably does more work on more gimped CPU hardware (AMD Jaguar consoles), but 100x real-time is pretty fast in my book. 😉
Source
The implementation is out there, but don’t expect to be able to use it as-is. This is a hobby project after all.
https://github.com/Themaister/Granite/blob/master/audio/dsp/tone_filter.cpp
https://github.com/Themaister/Granite/blob/master/tests/tone_filter_bench.cpp
VST plugin
I implemented a simple VST plugin with builds for Windows and macOS, both 64-bit. Feel free to try it out. It’s ultra bare bones.
EDIT: Old links were stale. Found the old code lying around in a private repo and made it public with the VST headers removed.
https://github.com/Themaister/ToneFilterVST
ToneFilterVST (Win64 build, untested)