I recently made a blog talking about how to properly filter pixel art in 3D, where I chose a cosine kernel as our low-pass. Please read through this to get a better idea of what I’m discussing here.
Pseudo-bandlimited pixel art filtering in 3D – a mathematical derivation
In this blog, I would like to analyze some alternative filters which we could potentially use, and try to explore the quality of the other methods from a signal processing standpoint.
“Ideal” sinc
The theoretical low-pass filter. Just as a reference.
Cosine
The filter kernel I chose as my filter.
d/dx (smoothstep)
I mentioned smoothstep in the previous post. smoothstep was mentioned as the integral of the filter kernel in many implementations, so to get the underlying filter to analyze, we take the derivative of smoothstep. Smoothstep is defined as 3x^2 – 2x^3. Its derivative is 6x – 6x^2, and if we normalize it to [-1, 1] range instead of [0, 1], we get:
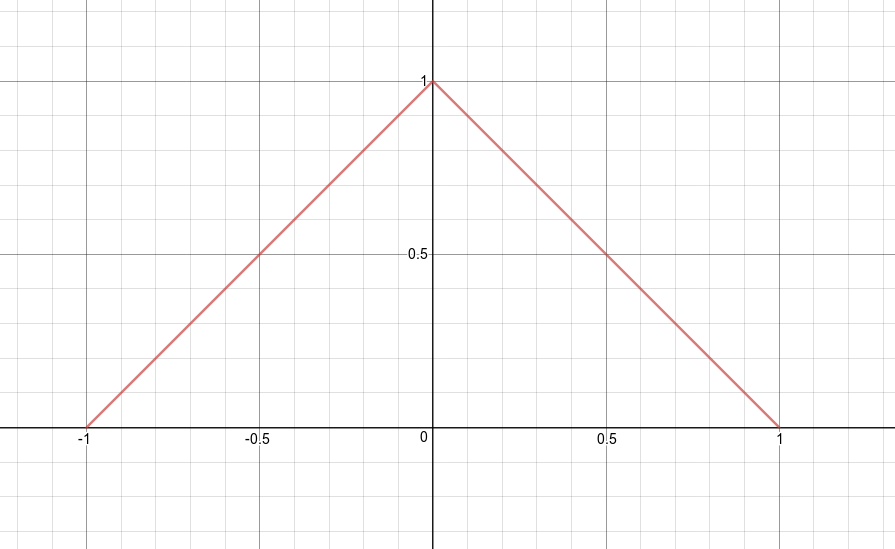
Triangle
The LINEAR filter. This is essentially the case we would get if we upscale pixel art a lot with NEAREST, then filter the result.
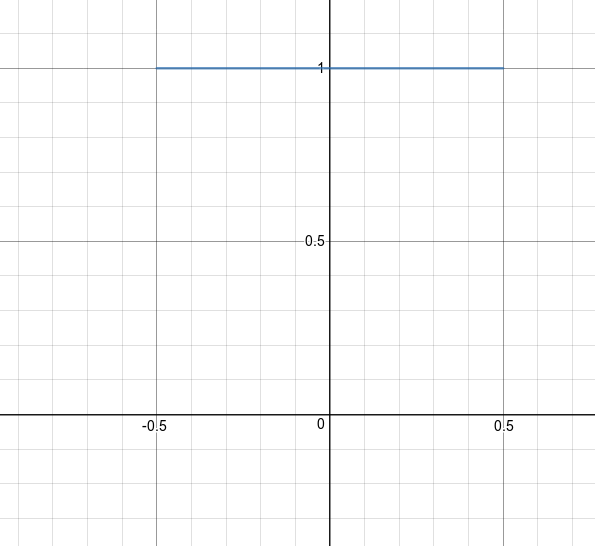
Rect
This is the worst low-pass filter ever as I mentioned in the last post. Interestingly, this is the filter we would use for coverage-based pixel art filtering if the texture and screen were aligned. (I don’t expect the result for rotated textures to be much different, but the rigorous analysis becomes a bit too hard for me). If our input signal is turned into a series of rects (pixel extent) ahead of time (which is what we do in our implementation), our coverage filter is basically the equivalent of convolving a rect against that signal. Basically, rect is the filter we would end up with if we cranked SSAA up to infinity.
One filter which implements this is (from what I can tell): https://github.com/libretro/slang-shaders/blob/master/retro/shaders/pixellate.slang
Windowed sinc (Lanczos2)
Lanczos2 is a fairly popular filter for image scaling. I’ve included it here to have some reference on how these filters behave in frequency space.
Filter response
Now, it’s time to drone on about the results. All of this on frequency response, stop bands, blah blah, is probably going to be too pedantic for purposes of graphics, but we can, so why not.
So, first we see the response around 0.5 in this graph. This is the Nyquist frequency. Our ideal sinc (or well – to be pedantic – a 16 lobe Hamming windowed sinc) falls immediately after 0.5. This is a completely impractical filter obviously.
Another consideration is how fast we reach the “stop band”, i.e., when the filter response has rolled off completely. Cosine and smoothstep are better here, while Lanczos2 is a bit slower to roll off. This is because of the window function. Applying a window function is the same as “blurring” frequency space, so the perfect sinc is smearing out too far. Linear and Rect don’t hit their first low-point until twice the Nyquist :(.
As for stop-band attenuation, windowed sinc is the clear winner, but again, this filter is impractical for our purposes (analytic windowed sinc integral with negative lobes breaking bilinear optimization? just no). Cosine seems to have a slight edge over smoothstep, with about 2 dB improvement. 2 dB is quite significant (For reference, halving root-mean-square error is ~6 dB). Triangle kernel (LINEAR filter) is about 3 dB worse again, and rect sniffs glue alone in the corner. Triangle and rect look very similar because a triangle kernel is just two rects convolved with each other, and thus its frequency response is squared (the more you know).
Conclusion
Cosine is a solid filter for what it’s trying to do, given our constraints on needing to analytically integrate whatever filter kernel we choose. The quality should be very similar to smoothstep, but I think I’ll consider cosine the winner here with 2 dB better stop-band attenuation. It also has slightly better response in the pass-band, which will preserve sharpness slightly better. This should make sense, because the cosine kernel has a higher peak and rolls of faster to zero than the smoothstep kernel. This frequency response can be expanded or contracted based on how we multiply the “d” parameter. Multiply it by 2 for example, and we have the equivalent of LOD bias +1.
Basically, coverage/area based filtering is pretty terrible from a signal processing standpoint. Rect is a terrible filter, and you should avoid it if you can.
Reference script
I captured this with Octave using this script for reference:
cosine_kernel = pi/4 * cos(pi/2 * (-1024:1024) / 1024);
windowed_sinc = sinc((-2048:2048) / 1024) .* sinc((-2048:2048) / 2048);
perfect_windowed_sinc = sinc((-64*1024:64*1024) / 1024) .* hamming(128 * 1024 + 1)';
rect_kernel = ones(1, 1024);
linear_kernel = conv(rect_kernel, rect_kernel) / 1024;
ramp = (0:2048) / 2048;
smoothstep_kernel = 3 * ramp - 3 * (ramp .* ramp);
cosine_fft = fft(cosine_kernel, 1024 * 1024)(1 : 16 * 1024);
windowed_fft = fft(windowed_sinc, 1024 * 1024)(1 : 16 * 1024);
perfect_windowed_fft = fft(perfect_windowed_sinc, 1024 * 1024)(1 : 16 * 1024);
rect_fft = fft(rect_kernel, 1024 * 1024)(1 : 16 * 1024);
linear_fft = fft(linear_kernel, 1024 * 1024)(1 : 16 * 1024);
smoothstep_fft = fft(smoothstep_kernel, 1024 * 1024)(1 : 16 * 1024);
offset = 20.0 * log10(1024);
cosine_fft = 20.0 * log10(abs(cosine_fft)) - offset;
windowed_fft = 20.0 * log10(abs(windowed_fft)) - offset;
perfect_windowed_fft = 20.0 * log10(abs(perfect_windowed_fft)) - offset;
rect_fft = 20.0 * log10(abs(rect_fft)) - offset;
linear_fft = 20.0 * log10(abs(linear_fft)) - offset;
smoothstep_fft = 20.0 * log10(abs(smoothstep_fft)) - offset;
x = linspace(0, 1024 * 16 * 1024 / (1024 * 1024), 16 * 1024);
figure
plot(x, cosine_fft, 'r', x, windowed_fft, 'g', x, rect_fft, 'b', x, linear_fft, 'b--', x, smoothstep_fft, 'k', x, perfect_windowed_fft, 'c-')
legend('cosine', 'lanczos2', 'rect', 'triangle', 'smoothstep', 'ideal sinc')
xlabel('frequency / sampling rate')
ylabel('Filter response (dB)')
xticks(linspace(0, 1024 * 16 * 1024 / (1024 * 1024), 65))